When considering throwing an object, two fundamental properties come into play: energy and momentum. Imagine throwing a light object and then a heavy object, applying what feels like the “same force” over an equal distance. In this scenario, both objects receive the same amount of energy (since energy is force multiplied by distance). However, their momentum will differ. Momentum is force multiplied by time. The heavier object, taking longer to accelerate with the same force, accumulates more momentum.
Interestingly, the heavier object will travel at a slower initial speed. The crucial question then becomes: which object will ultimately travel further? The answer hinges on the interplay between gravity and drag.
Case 1: When Gravity Predominates
For dense, compact objects like cannonballs, gravity is the dominant force affecting their trajectory. In such cases, the maximum distance the object will travel in the air largely depends on its initial velocity and launch angle. Ignoring air resistance for a moment, a launch angle of 45° maximizes the horizontal distance, given by the formula: d = v²/g (where ‘v’ is initial velocity and ‘g’ is acceleration due to gravity). This equation reveals a significant point: doubling the throwing velocity quadruples the range. In environments where drag is negligible, such as on the moon, lighter objects, thrown with the same energy, could potentially travel further due to achieving higher initial velocities.
Case 2: When Drag Takes Over
Consider lighter, less aerodynamic objects such as Nerf darts. For these, air resistance, or drag, becomes a critical factor. Drag force increases proportionally to the square of the velocity. This means doubling the velocity results in a fourfold increase in drag. Remember, heavier objects possess greater momentum. This leads to a counter-intuitive observation: a heavier object might travel further in scenarios where drag is significant. Because it starts slower, the heavier object experiences less drag initially. Moreover, the drag force has a proportionally smaller braking effect on an object with higher momentum. Even when a lighter object slows down to the same speed as a heavier one, it will continue to decelerate more rapidly due to its lower momentum being more susceptible to drag.
The Realistic Combination: Gravity and Drag Together
In reality, projectile motion is governed by a combination of both gravity and drag. This complexity means there’s no simple analytical solution to predict the distance the object will travel in the air. Numerical methods become necessary to accurately model these scenarios.
To illustrate this, consider objects of varying sizes and masses thrown with the same initial energy. Numerical simulations were conducted for objects with diameters of 1 cm (low drag), 5 cm (medium drag), and 20 cm (high drag), and masses ranging from 20 grams (light) to 2 kg (heavy). These objects were “thrown” at a 45° angle with a constant force applied over a distance of 1 meter.
The resulting trajectories are visualized in the plot below:
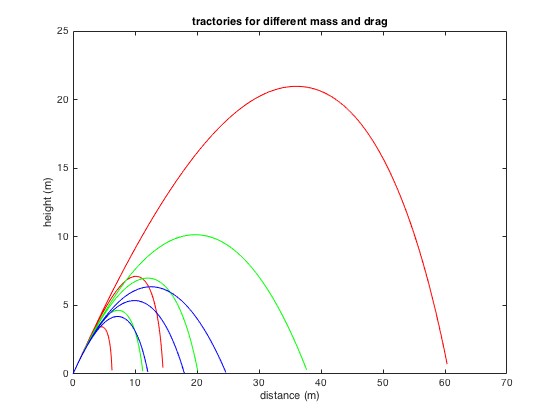Projectile trajectories demonstrating the influence of mass and diameter on travel distance, illustrating the interplay of gravity and drag.
In this graph, red lines represent 50g objects, green lines 150g objects, and blue lines 250g objects. Within each color group, the curves correspond to diameters of 5 cm, 15 cm, and 25 cm. As observed, the lightest object with the smallest diameter (red curve, lowest drag) initially travels the furthest. However, as drag increases (larger diameters), its range diminishes significantly. Conversely, while heavier objects with smaller diameters might not achieve the maximum range in low-drag conditions, they become advantageous as drag becomes more prominent. The heavier objects “win” in scenarios where air resistance is a significant factor influencing the distance the object will travel in the air.
This simulation highlights the intricate balance between gravity and drag in determining projectile motion and ultimately, The Distance The Object Will Travel In The _ air. Understanding these principles is crucial in various fields, from sports to engineering, where predicting and optimizing projectile trajectories is essential.
